Stopping Times and Laziness
A „Stopping Time“ is a certain type of random variable. Given a probability
space 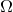 with a filtration
with a filtration _t.png) .
A random variable
.
A random variable 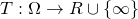 ,
is called a „stopping time“ iff
,
is called a „stopping time“ iff %20%5Cle%20t%5C%7D%20%5Cin%20F_t.png) for all t.
for all t.
What does that mean?
The filtration tells you what information is available at a given point t in time. A „stopping time“ is a random variable, where – at any given time t – you have enough information to decide, whether the random event happened or not.
Examples:
- „If it rains on Saturday, I'll go to cinema on Sunday.“ is a stopping time. On Sunday I have enough information to decide, whether it rained on Saturday or not.
- „If it rains on Sunday, I'll go to cinema on Saturday.“ is not a stopping time, since I cannot know on Saturday whether it will rain on Sunday or not.
Stopping times in real life
A simple application of stopping times are lazy sequences. Someone asked on the Clojure group to solve a certain problem fully lazy. However this was not possible, because the condition was not a stopping time.
In order to decide whether stop the current sequence and start processing the next one, one has to realise the next item of the input sequence. We have to know the weather of Sunday to decide on Saturday.
Upshot
You can be fully lazy if and only if your condition is a stopping time!
Published by Meikel Brandmeyer on .
About me
I'm a long-time Clojure user and the developer of several open source projects mostly involving Clojure. I try to actively contribute to the Clojure community.
My most active projects are at the moment VimClojure, Clojuresque and ClojureCheck.
Did you know about…
- … type hints?
- … some?
- … argument order?
- … version numbers?
- … comments?
- … bound-fn?
- … ::keywords?
- … -> and ->>?
- … with-open?
Archives
Copyright © 2009-2014 All Right Reserved. Meikel Brandmeyer




